Dominic Cummings has written a very interesting “essay for 15-25 year olds” entitled: Some Thoughts on Education and Political Priorities. http://static.guim.co.uk/ni/1381763590219/-Some-thoughts-on-education.pdf
It is well-argued and data rich, with an impressive scope. He includes many research findings on intelligence and education and social mobility. Von Neumann, Feynman, Kolmogorov, Turing, Newton, Poincare and Thucydides act as front runners for contemporary researchers such as Daniel Kahneman, Robert Plomin, Stephen Hsu, Alex Wissner-Gross and others. The essay combines a mathematical perspective with classical thinking to great effect. It does not lack ambition: there are good sections on mining, fuel utilization and power generation, solar photo-voltaic panels, digital fabrication, robots, developments in space exploration and sundry technical matters. There is much to enjoy for anyone who respects a factual approach to important social, technological and educational issues.
By way of example, in a footnote Cummings discusses Alex Wissner-Gross’ 2013 paper in Physical Review which attempts to describe intelligence as a fundamentally thermodynamic process, proposing that intelligence can spontaneously emerge from the attempt to maximise freedom of action in the future. He built a software programme designed to maximise the production of long-term entropy of any system it finds itself in. ENTROPICA then solved various problems including intelligence tests, playing games, social cooperation, trading financial instruments, and ‘balancing’ a physical system and so on. The key ingredient seems to be the maximisation of future histories. However, although the program models human and animal problem solving, it is not clear to me whether those outcomes arise from purely thermodynamic general principles. At the moment, I see this as self-criticism, and hope to post more on this research later.
As regards education, the main thrust of the book seems to be the need for random controlled trials and evidence-based teaching. To judge outputs you need to know the inputs. The ability level of your pupils at entry is one such key indicator. Schools have to be judged on the educational value they add. Methods need to change, targets should be set more ambitiously, and there should be more schooling days in the year. Teaching should pay attention to proven ways of learning, not just traditional methods like lecturing which burden short term memory. Approaches which are tailored to the child are championed.
Here is his educational thesis in a nutshell: The education of the majority even in rich countries is between awful and mediocre. A tiny number, less than 1 percent, are educated in the basics of how the ‘unreasonable effectiveness of mathematics’ provides the ‘language of nature’ and a foundation for our scientific civilisation and only a small subset of that <1% then study trans-disciplinary issues concerning the understanding, prediction and control of complex nonlinear systems. Unavoidably, the level of one’s mathematical understanding imposes limits on the depth to which one can explore many subjects. For example, it is impossible to follow academic debates about IQ unless one knows roughly what ‘normal distribution’ and ‘standard deviation’ mean, and many political decisions, concerning issues such as risk, cannot be wisely taken without at least knowing of the existence of mathematical tools such as conditional probability.
Here is his charge sheet on English education in the last 30 years:
Large improvements in state-controlled test scores have not been matched by independent tests. Durham University found that the GCSE grades of pupils who sat PISA in 2009 were higher than those of pupils who got the same PISA maths score in 2006 (which they should not have been, of course).
A major study found a significant decline in the algebra and ratio skills of 14 year-olds between 1979 and 2009: fewer than 1/5 of 14 year olds can write 11/10 as a decimal.
Pupils in the top tier of countries (Shanghai, Singapore, et al) are about 1-2 years
ahead of English pupils in the PISA maths.
TIMSS (a more curriculum-focused international maths test) also shows England behind at primary school and the gap widening with age.
A 2011 BIS survey of adults found that only ~1/5 operate in maths at a level of a GCSE ‘C’ or better. Research from National Numeracy (February 2012) showed that
~½ of 16-65 year olds have at best the mathematical skills of an 11 year-old.
Before the EBac, only ~1/8 of those at a non-selective state school got a C or better GCSE grade in English, Maths, two sciences, history or geography, and a language (~½ of privately educated pupils do).
GCSEs are poor: cf. the Royal Society’s 2011 study of Science GCSEs, Ofqual’s April 2012 report, and damning analysis from the Institute of Physics and Royal Society of Chemistry. Shayer et al (2007) found that performance in a test of basic scientific concepts fell between 1976 and 2003.
Many University courses, including Cambridge sciences, had to lengthen from the 1990s to compensate for the general devaluation of exams.
Foreign languages are in crisis even in Oxbridge: forty years ago, interviews were conducted in the language, now tutors are happy if an applicant has read anything in the language. For a recent survey, cf. Coe (2013).
Only 1.7% of 15-year-olds in England achieved Level 6 in PISA 2009 maths tests compared with: Shanghai (27%), Singapore (16%), Hong Kong (11%), South Korea and Switzerland (8%), Japan (6%), Finland and Germany (5%). If one
looks at Levels 5 and 6, only 10% in England reach this level compared with: Shanghai (50%), Singapore (36%), Hong Kong (31%), South Korea (26%), Switzerland (24%), Finland (22%), Japan (21%). Given that those from independent
schools score >50 points higher than those from maintained schools, the tiny English 1.7% may include a large overrepresentation of independent schools and the performance of pupils in non-grammar state schools may be worse than these figures suggest.
During my involvement in education policy 2007-12, I never come across a single person in ‘the education world’ who raised the work of Robert Plomin and others on IQ, genetics and schools, and whenever I raised it people would either ignore it or say something like ‘well obviously IQ and genetics has no place in education discussions’. I therefore invited Plomin into the DfE to explain the science of IQ and genetics to officials and Ministers.
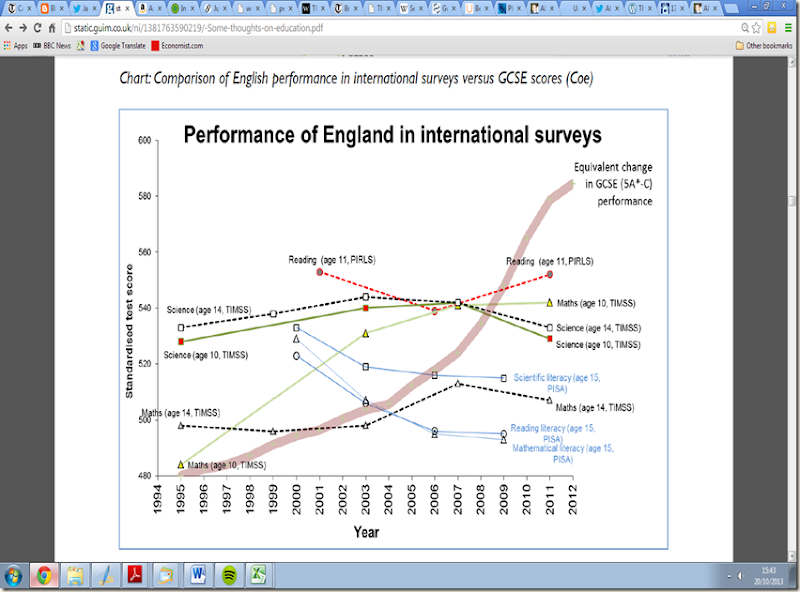
Here is the summary picture, which casts significant doubt on GCSE results:
Nothing particularly surprising about all of that, at least to those who have some knowledge of the intelligence literature. Not all of those difference may be entirely due to bad teaching. If one takes “school far” tests based on the sorts of things any student is likely to know regardless of the particular curriculum, then Chinese and Japanese do well on those tests, as well as those that are “school near” and depend on specific teaching. The former are sometimes called ability or intelligence tests. The same intelligence differences can be found in occupational classes.
There is huge variation in school performance (on exams that are sub-optimal) among schools with the poorest children. In about a quarter of primaries over a quarter of pupils leave not properly prepared for basic secondary studies (and few such pupils enjoy a turnaround at secondary school). Other primaries, including those in the poorest areas) have have fewer 5% of their pupils in such a
desperate situation.
Consider a basic benchmark: getting four-fifths of pupils to at least a ‘C’ in English and Maths GCSE. A small minority of state schools achieve this, while others with
similar funding and similarly impoverished pupils struggle to get two-fifths to this level.
It is a sign of the fundamental problems with ‘education research’ that the Institute of Education is very hostile to research on genetics and education.
When people look at the gaps between rich and poor children that already exist at a young age (3-5), they almost universally assume that these differences are because of environmental reasons (‘privileges of wealth’) and ignore genetics.
It is reasonable to hope that the combination of 1) finding the genes responsible for cognitive abilities, 2) scientific research on teaching methods, and 3) the power of computers to personalise learning will bring dramatic improvements to education - but this will not remove genetic influence over the variation in outcomes or ‘close the gap between rich and poor’. ‘The good school ... does not diminish individual differences; it increases them. It raises the mean and increases the variance’ (Elliot Eisner, Stanford). Good schools, in the sense of ‘teaching children of different
natural abilities as well as possible’, will not ‘eliminate gaps’ - they will actually increase gaps between those of different abilities, but they will also raise floors and averages and give all children the opportunity to make the most of their genetic inheritance (personality as well as IQ).
Education is political battlefield. It is seen as a very powerful influence on society, and the benefits of different types of education are not judged on merely pragmatic grounds but as part of a wider pattern of social change. From an empirical point of view this raises many problems. If you think some purveyors of education are better than others, this will be seen as taking a political stance. Any book which reports results and makes policy proposals cannot help but be political, and to be judged by those standards. Education systems tend to be evaluated by intentions, not outcomes.
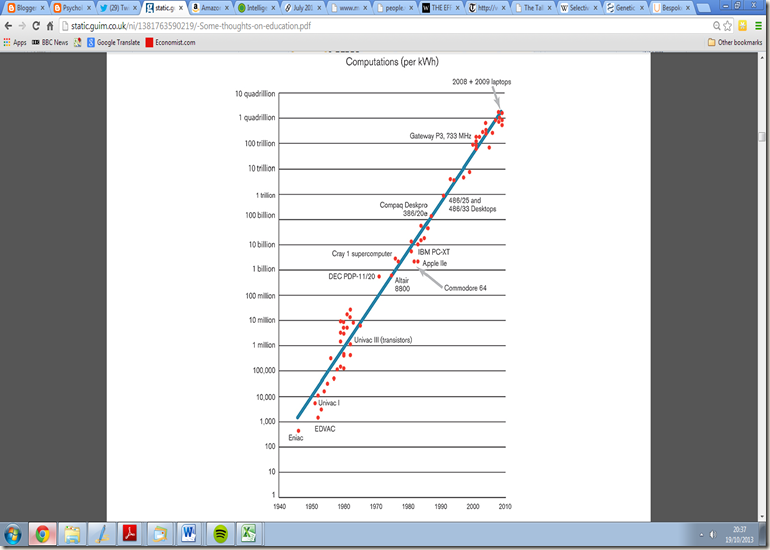
In a pleasant contrast, here is a graph showing a real improvement in the mental tools at our disposal.
I note that the Apple IIe which was my first home computer in 1982 or thereabouts was operating at the same level of efficiency of the then mighty Cray 1 computer, and the Compaq 386 I had by the late 80s was very quickly surpassed. Current desktops operate at the power of the fastest supercomputers in 1993. More impressively, if you took the top 500 computers in 2008, their combined power was surpassed by the best single supercomputer in 2013. Smartphones are about as powerful as the best computers of 25 years ago. The point is not that my word processing speed has increased, but that analysis of all sorts became feasible, such that you can design a wide body jet without using a wind tunnel, and get it to fly properly. Genome sequencing is becoming easier at a rate which is faster than Moore’s Law. You can also just about begin to interpret the genome, though that may take more power and much larger samples. Incidentally, much of the improvement in processing problems comes from better algorithms, not the chips. However, current computation cannot yet compete with the estimated 1017 floating point computations, for the mere expenditure of 20 watts, achieved by the human brain. Modelling that will take a fair bit of computer power, possibly not available till after 2020.
In sum, Cummings has written a very interesting, informative and inspiring essay, which gathers together many of the ingredients required to think about our changing technical and organisational world. His parting gift is an Odyssean reading list for young students. His essay is an exciting read in the grand tradition of two cultures, covering a broad canvas with a sense of adventure and a love of discovery.

When I was clearing up my office before retiring, a colleague pottered in to see what I was binning. Aha, he said, picking up some yellowed lecture notes, Field Theory. When did you study this?
ReplyDeleteFreshman physics, said I.
It's now a second year course, he said, and too tough for the core lectures - it's an option.
And that, children, is why what was once a three year physics course now takes four. It has nothing to do with "frontiers" having advanced. It has everything to do with The Forces of Progress succeeding in their project to bugger up the schools.
Glad you enjoyed Cummings's piece.
ReplyDeleteOn a related note, similar thoughts were running through my head my last when I got back from tutoring an extremely bright boy last night. He's recently moved schools and his previous school didn't teach Latin so he's temporarily behind his class (hence the tutoring). It's easy to see, however, that he'll catch up and leap ahead in no time at all. The problem is that, given competent teaching (admittedly something of a rarity when it comes to Latin), the standardized exams are simply too easy for boys of his intellectual powers. Common Entrance scholarship is barely distinguishable from GCSE, but material that was set for unseen translation at O-level in the 1980s is now given as a "set" (i.e prepared) text at GCSE, which shows how far the latter exam has become degraded. Your average prep school boy will start learning Latin at perhaps age 10 and not sit the GCSE until age 15/16. Even those of more average intellects could easily go from beginner to GCSE level in 3 years; those like this young man could do it in 2 or even 1. We have fallen a long way from the days when 1850s-era textbooks of Greek, created for the instruction of pupils at Eton, were written in Latin.
At this point, the exams themselves do not offer any method of discrimination between the extremely bright and hard-working and the merely hard-working. The examiner cannot see the differing amount of effort each boy has to put in to achieve the same (top) grade - only I can. And many schools, for a variety of reasons, do not allow precocious children to take exams early, so age at a certain level of performance is not usually an accurate guide to intellect either. This rather suggests that the exams are simply not doing their job.
Admittedly, the Latin teaching community does its best to remedy these problems and keep their pupils entertained by teaching them in a truly appalling fashion, thus ensuring that they aren't ready for the exams too early. The widely used Cambridge Latin Course is an appalling pile of dreck that fails to teach even the rudiments of grammar. Any pupil who manages to do well in any exam after having been taught from that thing is clearly of above-average intellect - so perhaps the exams do retain some predictive validity after all.
I cannot advise you about Latin, unfortunately. As a Spanish speaker I could not see what it offered when I was being taught it, to my shame, and turned to other things. Sorry you don't rate the Cambridge Latin Course which, in my ignorance, I might have mentioned. However, I have a general suggestion. If your pupil can rise to Latin verse, then he could submit it for comment to Westminster School, and now that since 2005 they have a wider set of bursaries they might be able to give advice and perhaps give some extra help. Then your candidate could take the exams, feeble as they may be, but could add that they had achieved a prize in Latin, or attended a summer school, thus showing his extra abilities. Six Westminster scholars in the top set were accorded entry to Trinity College if they composed a Latin ode of quality, but for unaccountable reasons this practice has been discontinued in recent times.
ReplyDeleteI read that Post and got it fine and informative.
ReplyDeletemath tutor
Thank you
ReplyDeleteIt is reasonable to hope that the combination of finding the genes responsible for cognitive abilities, scientific research on teaching methods. And the power of computers to personalize learning will bring dramatic improvements to education.
ReplyDelete